在翻阅Aave-V2的白皮书的时候，有一章节在讲gas优化的，其中的一些思路值得效仿学习一下

幂运算优化

在借贷系统中，很多场景涉及到复利率低计算功能，由于这是个幂运算的过程，如果幂数过大会导致计算的迭代次数变多，会增加gas的消耗和性能的降低，在通过对复利公式做二项式展开得到如下公司

$$ (1+x)^α =1+αx+ \frac{1}{2}α(α−1)x^2 + \frac{1}{6}α(α−1)(α−2)x^3 + \frac{1}{24}α(α−1)(α−2)(α−3)x^4 +… $$

会发现，只要保留前三阶项的展开就能满足5年以内的复利率精度

因此我们要计算的的项只有如下

$$ (1+x)^α \approx 1+αx+ \frac{1}{2}α(α−1)x^2 + \frac{1}{6}α(α−1)(α−2)x^3 $$

function calculateCompoundedInterest(
    uint256 rate, // 年化利率
    uint40 lastUpdateTimestamp, // 利率计算开始时间
    uint256 currentTimestamp // 当前时间
  ) internal pure returns (uint256) {
    //solium-disable-next-line
    uint256 exp = currentTimestamp.sub(uint256(lastUpdateTimestamp));

    if (exp == 0) { // 时间间隔为0，利息不变就是1
      return WadRayMath.ray();
    }

    uint256 expMinusOne = exp - 1;

    uint256 expMinusTwo = exp > 2 ? exp - 2 : 0;

    uint256 ratePerSecond = rate / SECONDS_PER_YEAR; // 年化利率除一年的秒数

    uint256 basePowerTwo = ratePerSecond.rayMul(ratePerSecond);
    uint256 basePowerThree = basePowerTwo.rayMul(ratePerSecond);

    uint256 secondTerm = exp.mul(expMinusOne).mul(basePowerTwo) / 2;
    uint256 thirdTerm = exp.mul(expMinusOne).mul(expMinusTwo).mul(basePowerThree) / 6;

    return WadRayMath.ray().add(ratePerSecond.mul(exp)).add(secondTerm).add(thirdTerm);
  }

移除对SafeMath的引用

之前的V1版本直接用了OppenZeeplin的SafeMath，导致在做大量的数学运算的时候额外增加了不必要的消耗，V2的版本改成了直接自己在代码库内实现相关的安全数学操作

BitMask的使用

用户的借贷信息存储

使用一个256Bit的整数，两两Bit成一对，每一对代表对应的资产，第一个Bit用来表示用户是否用该资产来做抵押物，第二个Bit表示用户是否借用该资产

Untitled

在V1的版本中是用了List来存放用户的相关信息，相关的操作会比较消耗gas

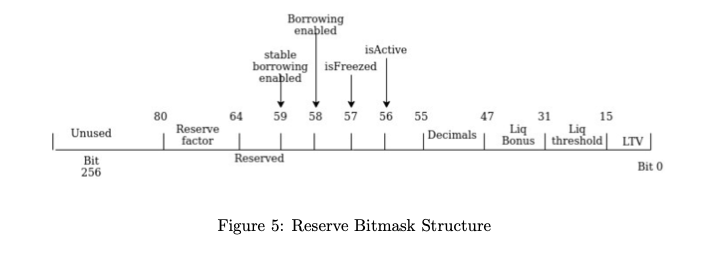
配置管理

一些配置只涉及二元逻辑的，实用bitmask来管理，不仅节省gas，在针对多个配置操作的时候还能支持并发的操作

AAVE-v2-reserve-bitmask

总结

优化都是要经过深度的分析之后才有必要去做，不然都是费时费力不讨好的事情

  • 部分优化其实都是迫于当前solidity编译器不是很智能而去做的，比如 SafeMath的引用优化这块
  • 针对智能合约的场景，当用户体量大了之后，gas的优化会变得尤其重要

参考

https://github.com/aave/protocol-v2/blob/master/aave-v2-whitepaper.pdf